Acceleration in one-dimension
Variant i Interactive tutorial lecture Other Variants Dynamics first, Conservation laws first
Students interpret and apply operational definitions of velocity, change in velocity, and acceleration. There is an emphasis on vector addition and subtraction.
Topics Mechanics / Kinematics: graphs, idealizations, limits, operational definitions, rates of change, representations, vectors, acceleration, acceleration vs. velocity, change in velocity, kinematics, slopes of graphs, and vector addition & subtraction
Materials
Materials by the UW team
- Clicker Questions Only

- Instructor Guide

- Pretest


- Pretest for LMS


- Exam Questions


- Equipment List

Tutorial details
Students apply the operational definition of acceleration to specific situations.
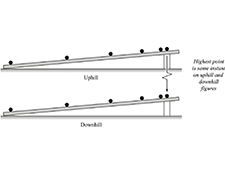
Section I: Ball rolling up a ramp
Question A guides students in drawing velocity vectors for a ball moving up an incline. They then draw vectors for two sequential instants side-by-side and find the vector that must be added to the earlier velocity to obtain the later velocity.
In Question B students consider how the change in velocity depends on the time interval. They are given a velocity vs. time graph and guided to recognize that the change in velocity is proportional to the elapsed time and thus, the acceleration is constant.
Question C establishes the relationship between the direction of acceleration and the direction of velocity for an object that is moving in a straight line and slowing down.
Section II & Section III:
Students repeat the reasoning above for a ball moving down the incline and near the turnaround. Some may be surprised that the acceleration is not zero at the turnaround.
Finally, students extend the velocity vs. time graph from Section I to include the motion down the incline.
Section IV: Supplement
In the supplement, students apply the ideas from the prior parts of the tutorial to the case of an object colliding with a wall.
For instruction tips, login or register as a verified educator to see the Instructor Guide.
Prerequisites
Prerequisite tutorials
The Representations of motion tutorial is a prerequisite to Acceleration in one-dimension.
Other prerequisites
Students should have been introduced to vectors and the definitions for velocity and acceleration. It is not required that they know that an object on an incline has constant acceleration.
Research
Many students fail to relate acceleration to changes in motion, instead reasoning about underlying forces or causes of the motion. Although this can, in some cases be useful, often the acceleration or its direction must be inferred from the motion.
Research also indicates that many students have difficulty with vector operations and thus fail to find acceleration correctly from the initial and final velocity. This tutorial uses one-dimensional motion to lay the groundwork for finding acceleration in two dimensions in a later tutorial.
- P. Shaffer and L. McDermott, A research-based approach to improving student understanding of the vector nature of kinematical concepts, Am. J. Phys. 73 (10), 921 (2005).
- D. Trowbridge and L. McDermott, Investigation of student understanding of the concept of velocity in one dimension, Am. J. Phys. 48 (12), 1020 (1980).
- D. Trowbridge and L. McDermott, Investigation of student understanding of the concept of acceleration in one dimension, Am. J. Phys. 49 (3), 242 (1981).
Coming Soon! We hope to release the discussion section on each tutorial soon.

