Tutorial details

Students begin by developing a definition of the area vector for a surface. Students compare the area vector for a flat sheet of graph paper to the area vectors for each of the individual squares on the sheet. Students then consider the minimum number of area vectors required to represent the surface of a hollow triangular tube, and then of a cylindrical tube. Many students have difficulty with the idea that, if a smoothly curved surface is divided into sufficiently small portions, each portion can be considered to be flat. It may be helpful to ask students to consider a portion of the Earth’s surface. (e.g., Can you consider the surface of a small lake to be flat?)

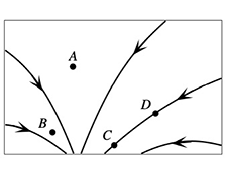
In the second section of the tutorial, students define the electric field as a ratio of the electric force on a test charge to the charge of the test charge. They are led to recognize that the magnitude and direction of the electric field do not depend on the test charge. The electric field line representation is then introduced. Students use the results of previous exercises to identify which features of the field lines reflect information about the direction and strength of the electric field.

In section III, students develop a definition for electric flux through a flat surface. They should be given a block of wood with nails through it to represent a uniform electric field, and a wire loop to represent the surface. Students use this equipment to graph the number of “field lines” (nails) through the loop versus the angle θ between the area vector and the field lines. The maximum flux is defined as E times A (where E is the magnitude of the electric field at the surface and A is the surface area). Students are then asked which trigonometric function gives the appropriate relationship between the maximum flux and the flux at an angle θ. They are then guided in re-writing their result as a vector relationship.

For instruction tips, login or register as a verified educator to see the Instructor Guide.

Prerequisite tutorials

The Charge tutorial is a prerequisite to Electric fields and flux.

Other prerequisites

It is expected that students have worked through the tutorial Charge. Students should be familiar with using vectors to represent an electric field. No knowledge of electric field lines, electric flux, or Gaussian surfaces is assumed.

Equipment

List

• fur or cloth (for charging rods)
• graph paper
• plastic rods (approx. ~ 0.5" diameter by 10" long)
• protractor
• white board or large sheet of paper with markers
• small pieces of paper such as 3" x 5" index cards
• pith ball [small Styrofoam balls (~ 1 cm diameter) covered with aluminum foil and hung from fine insulating (e.g. polyester) thread]

Discussion