Research-based worksheets for introductory physics that help students
-
build on their own good ideas as “seeds of science”,
-
engage in sense-making about physics, and
-
develop and apply models of key physics concepts.
Open-access and editable so you can customize for your classroom and students.
Get the ACORN Physics Tutorials
View and download FREE worksheets, discussion questions, and instructor guides for these topics in introductory physics:
 Circuits Tutorial
Circuits Tutorial
 Momentum Tutorial
Momentum Tutorial
 Waves Tutorial
Waves Tutorial
 Heat & Temp. Tutorial
Heat & Temp. Tutorial
Design and structure of ACORN Physics Tutorials
ACORN Physics Tutorials are worksheets that students work on collaboratively in groups of 3-4 with support from instructors and/or near-peer facilitators. Each takes 50-90 minutes for students to complete. Three types of questions guide students to build their own models for common physics phenomena:
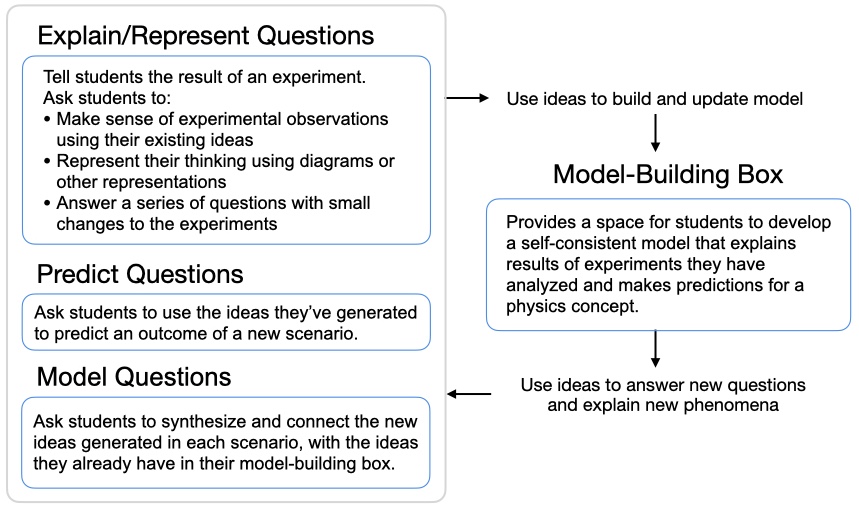
To learn more, see instructor resources.
Introduction
 Here is a series of conceptual questions that draw out a variety of conceptual resources, which are potentially generative student ideas or “seeds of science” that can grow toward sophisticated understandings with support and cultivation. These questions could be used as discussion questions in an introductory physics course, or as homework or quiz questions. We recommend using these when beginning a new topic, to learn about your students' ideas. Many of these questions are featured in ACORN Physics Tutorials, but some are not and could be used in conjunction with the Tutorials to further advance resources-oriented instruction. For each question, we include:
Here is a series of conceptual questions that draw out a variety of conceptual resources, which are potentially generative student ideas or “seeds of science” that can grow toward sophisticated understandings with support and cultivation. These questions could be used as discussion questions in an introductory physics course, or as homework or quiz questions. We recommend using these when beginning a new topic, to learn about your students' ideas. Many of these questions are featured in ACORN Physics Tutorials, but some are not and could be used in conjunction with the Tutorials to further advance resources-oriented instruction. For each question, we include:
- A downloadable (and editable) PowerPoint slide with the question.
- Information for instructors about the question design and our answer to the question.
- A few sample student responses and an overview of some of the conceptual resources we observe students using and how we perceive these resources to be connected to introductory physics learning goals.
Linear momentum questions
 Ball/clay predict question
Ball/clay predict question
The ball/clay predict question tells students to suppose they want to close a door quickly but cannot reach it. The question then asks whether they would choose to throw a rubber bouncy ball or an equally massive piece of clay at the door to accomplish this task.
Information for instructors:
The ball/clay predict question is a predict-style question, a type of question that asks students to apply principles and ideas to a new scenario. Our own answer to this question is that the ball will move more quickly if we choose to throw the rubber bouncy ball. With the door initially at rest, the initial momentum of the system is the momentum of the clay/ball. If we assume these initial momenta are the same (e.g., we throw them with the same speed in the same direction and they are equally massive), then the vector representing the momentum of the system points in the same direction and is the same length for both scenarios. The clay sticks to the door and continues to have a component of motion in its original direction, and the rubber ball bounces and moves in the opposite direction. By vector addition, the final momentum of the door (which moves in the ball’s original direction of motion) would be higher with the rubber ball.
Common ideas and sample student responses:
Students used a variety of conceptual resources in their responses to this question, ranging from applying rules and constraints they may have learned in physics class (using terms like “isolated system,” “momentum conservation,” and “elastic and inelastic collisions”), to sense-making about what an inelastic or elastic collision is (drawing on ideas of force and energy). For example, one student wrote:
“The momentum when it approaches the door is positive. Assuming this happens in a closed system, momentum is conserved. So, when the bouncy ball hits the door, it moves in a negative direction & has a negative momentum, causing the door to have a positive momentum in the opposite direction.”
This (correct) written student response illustrates attention to both the conservation and the directionality of momentum at different moments during and after the collision.
Another student wrote:
“The [motion of the door will be the] same. When they [rubber ball and clay] collide the door, the momentums of the door change in the same magnitude because they have the same mass.”
This student reasons that since the rubber ball and clay are equally massive, the door they hit will experience equal changes in the magnitudes of momentum. While this response is canonically incorrect, the student is both (i) considering a property of the objects (mass) that are relevant to momentum and (ii) recognizing that the properties of the object matter for what happens in a collision between them. Many students used similarly structured arguments, reasoning that because the objects that collided have a certain property (hard, soft, bouncy, heavy, light, fast, etc.), their momentum changes in a certain way.
Some students provided a mechanism that explained why they thought either the rubber ball or the clay would shut the door more quickly. For example:
“I would throw the piece of clay at the door because it wouldn’t bounce off as much. More momentum would be transferred from the clay.”
This student (and others like them) reasoned that because the clay stuck to the door, it transfers more of its momentum to the door. Other students answered that the bouncy ball has more oomph and so transfers more of its momentum to the door, or that bouncy objects can change their momentum more.
In short, the ball/clay predict question appears to elicit resources for conservation, directionality, and identifying the kind of collision at play, as well as mechanisms that students use to explain why one collision or the other might transfer more energy or momentum.
 Desk chair momentum predict question
Desk chair momentum predict question
The desk chair momentum predict question tells students that two people are facing one another in desk chairs with low-friction bearings and that one of the people tosses a large, heavy ball to the other. They are asked whether the student who tosses the ball will remain at rest, and whether the student who catches the ball will remain at rest.
Information for instructors:
This predict-style question is similar (but not identical) to questions found on the Energy and Momentum Conceptual Survey and the Force and Motion Conceptual Survey. Our answer to the desk chair momentum predict question is that the student who tosses the ball will begin moving opposite the direction they toss the ball, and the person who catches the ball will begin moving in the direction of motion of the ball as they catch it. We can make sense of the catcher’s movement in terms of momentum transfer: when the ball collides with the person, it gives some of its momentum to the person, and they begin to move. The ball and the person move more slowly than the ball did originally because of momentum conservation: when the ball gives some momentum to the person, it moves slower. The person is presumably more massive than the ball and receives only a part of the ball’s momentum so also moves slower than the ball did. For the thrower: the original (vector) momentum of the system was zero. When the ball moves one way, the thrower must move the other way to conserve momentum.
Common ideas and sample student responses:
The desk chair predict question elicited a variety of resources, often relating to momentum conservation and transfer. Some of these resources resembled rules or procedures: momentum is conserved, momentum can transfer, analysis of systems, or efforts to “balance” or “equalize” momentum (connected to, but not precisely, momentum conservation). Others resembled mechanisms for momentum transfer (e.g., forces). For example:
“No. They will both move farther apart. For the first, momentum one way leads to momentum the other way. Second, the momentum of [the] ball transfers to the person.”
This response uses a sort of “momentum balancing,” reminiscent of (and a resource for) momentum conservation, to determine that the thrower will move opposite the direction of motion of the tossed ball. They use momentum transfer (which implies conservation) to decide that the catcher will also move.
Another student responded:
“If you break the situation into two different systems: the thrower and the catcher, the thrower system is elastic and the catcher system is inelastic. This helps us because when looking at the thrower system, the thrower is initially at rest but then when throwing the ball we know that momentum needs to be conserved so the student will move backwards canceling out the motion of the ball. Then when the other student catches both the student and ball ‘stick’ together and move in the same direction.”
This response draws on a variety of resources, including identifying systems, to conclude that both the thrower and the catcher will move. They name two relevant systems for this scenario – (1) the thrower and the ball and (2) the catcher and the ball – and identify one collision as elastic and the other as inelastic. Though it’s not totally what this student means by “elastic” and “inelastic,” they are drawing on resources for identifying systems and types of collisions that connect with learning objectives in introductory physics in ways that instructors might build on.
Some students drew on Newton’s third law to make sense of the direction of motion of the thrower and the catcher. For example:
“No - neither remains at rest. Both catching and throwing the ball requires a force and these forces come in equal/opposite pairs, so applying a force to move the ball/slow it down will also apply a force to you in the chair that moves you.”
Here, the student argues that as the thrower applies a force to move the ball, the ball exerts an equal and opposite force on the person, such that the person will move (accelerate) in the direction opposite the ball’s motion. Likewise, when the catcher applies a force opposite the ball’s motion to slow it down upon catching it, the ball applies an equal and opposite force to the catcher, accelerating the catcher in the direction of the ball’s motion.
In summary, the desk chair momentum predict question appears to elicit resources for momentum conservation and transfer, as well as resources that connect forces and energy to momentum, all goals of introductory physics instruction in the context of linear momentum.
Circuits questions
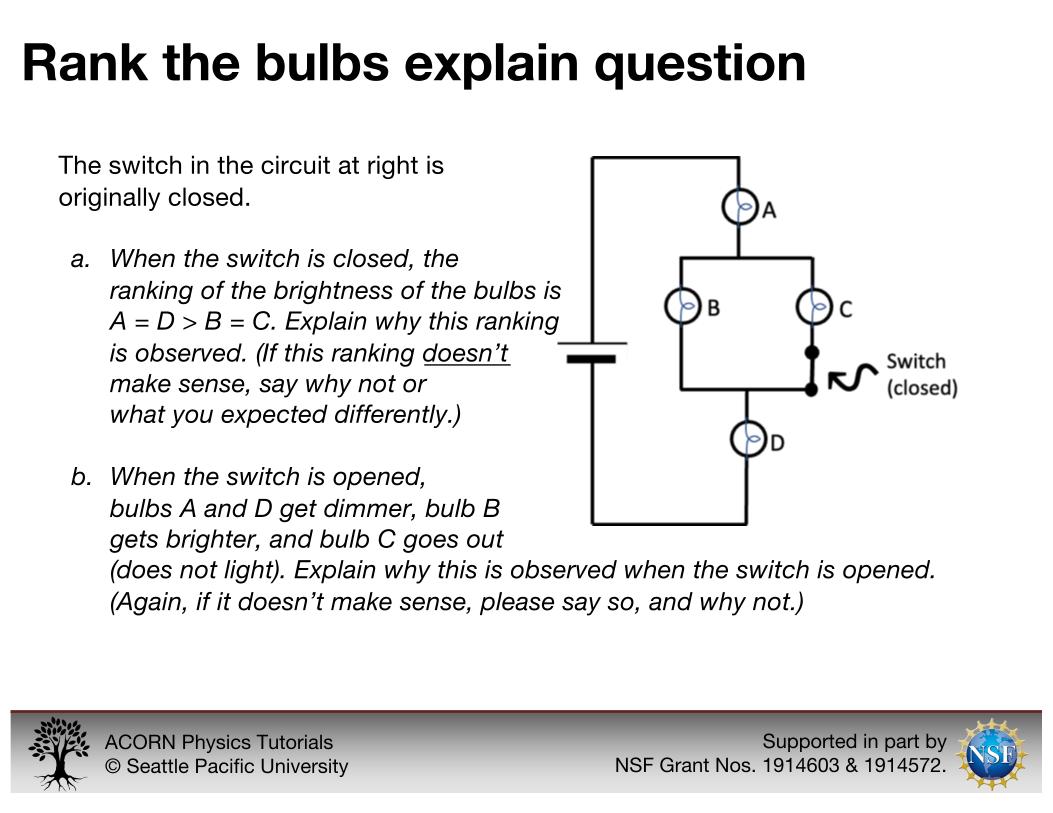
 Rank the bulbs explain question
Rank the bulbs explain question
The rank the bulbs explain question shows students a circuit with four bulbs and a switch, and ranks the brightness of the bulbs when the switch is closed (part a) and then opened (part b). Students are asked to say why the rankings are observed.
Information for instructors:
This question is featured in our ACORN Physics circuits tutorial and in our research (Bauman et al. 2024), and in using it there and elsewhere, we sometimes find that it can help to break question (b) into several parts, highlighting the dimming of bulbs B and C, the brightening of bulb A, and bulb D going out altogether separately. This is an explain-style question that describes a phenomenon and asks students to sense-make about it, rather than to predict a particular outcome. It was adapted from McDermott and Shaffer 1992. Our own answer to this question relies on current tracing and Ohm’s Law: in the original (closed switch) circuit, all of the current from the battery goes through bulb A, then splits equally through bulbs B and C (which are identical), then recombines to go through bulb D. This makes B and C equally bright but dimmer than A and D, which are themselves equally bright (since the current is conserved as it splits and recombines). When the switch is opened, the branch with bulb C is no longer complete, and what was originally a two-bulb parallel circuit element becomes a single-bulb series element, such that the circuit is effectively a three-bulb series circuit. This increases the resistance, decreasing the current through the battery. Thus bulbs A and D, which originally received all of the current from the battery, dim. Bulb B, now in series with the battery, brightens, and bulb C does not light.
Common ideas and sample student responses:
Students used a variety of resources for understanding current, voltage, and resistance to answer this question. Most commonly, students focused on current as responsive to changes in the circuit (including different connections) and resistance as limiting current. For example:
“...when the switch opens, bulb B joins the series instead of just being in parallel to bulb C, so resistance increases. The battery is the same so V remains the same. Therefore current must decrease to compensate.”
This response acknowledges that the way the circuit elements are connected matters for the properties (in particular, the resistance) of the circuit, naming that the resistance increases if you take away a parallel branch. The student draws on the resource that current is responsive to changes in the circuit; when voltage remains the same but resistance increases, “current must decrease to compensate.”
Another student wrote:
“When the switch is opened, the current no longer has the option to split and flow through either B or C, it must all flow through B. Since B and C are no longer in parallel, the overall resistance of the circuit is greater than when the switch is closed. With greater resistance, there is less current according to Ohm’s Law. And since the luminosity of a light bulb is directly proportional to current, this means dimmer light bulbs as well.”
Here, the student uses current tracing (conservation of current) to analyze how changing the connections in the circuit will change how the current moves through. Like the previous response, this student acknowledges that removing a parallel branch increases the resistance of the circuit, which increases the current by Ohm’s Law.
As might be expected with complex circuits that contain many elements, students’ analyses in the rank the bulbs explain question include multiple parts that include a variety of resources. We are especially interested in the ways in which these responses articulate a nascent conceptual model of current as responsive to changes in the circuit (including changes in resistance and changes in how elements are connected to one another), a resource that appears to be consistently activated in this context.
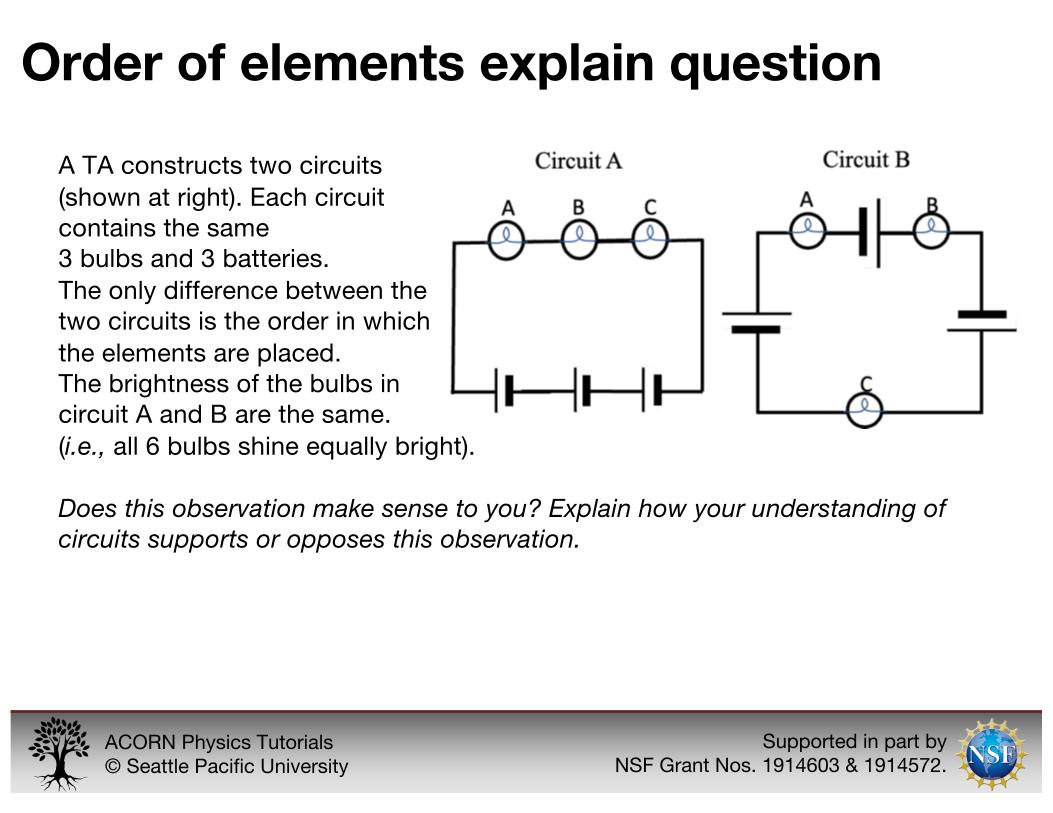
 Order of elements explain question
Order of elements explain question
The order of elements explain question shows students two circuits, both of which have three batteries and three bulbs in series, with all of the batteries facing the same direction. However, in the second circuit, rather than having three bulbs then three batteries in a row, the elements are arranged bulb-battery-bulb-battery-bulb-battery. Students are told that all six of the bulbs in the two circuits are equally bright and are asked why this is the case.
Information for instructors:
The order of elements explain question is an explain-style question that asks students to make sense of the observation that the order of batteries and bulbs in a circuit does not impact the brightness of the bulbs.
Common ideas and sample student responses:
As with the rank the bulbs explain question, students drew on resources that highlighted that current is responsive, this time also foregrounding that voltage drives current, alongside attending to resistance as opposing current and the connections between elements as relevant. For example:
“[...] In circuit A, the batteries are all in a row which increases the total current but the resistors are also in a row which would decrease the total current. Circuit A has 3 times the voltage but also 3 times the resistance, which would result in the same current. Circuit B also has the same current because the voltage is one and the resistance is 1, but it happens three times in series.”
Though it isn’t clear to us how this student calculated the voltage and resistance (as 1 for Circuit B, and as “three times” for Circuit A), it is clear that they are framing voltage as driving current, resistance as limiting it, and current as responsive to both. It may be that they think of the current as going up and then down (changing as it moves through the circuit); whether or not this is the case, we can identify resources in this response that we could leverage to support conceptual understanding of voltage, current, and resistance.
Similar notions of voltage as driving current and resistance as limiting it are observed in this student response:
“[It] makes sense [that all the bulbs are the same brightness] because the current is the same everywhere in the wire and is being pushed forward by the same amount of voltage from the batteries and resisted by the same amount of resistance.”
This student justifies not only that the current should be the same in the two circuits, but also that the current should be the same throughout each circuit, using language of “pushed” (for voltage) and “resisted” (for resistance).
Some students focused on the two circuits having similar types of connections (rather than, say the same numbers and types of elements). For example:
“[...] Since electrons flow as a stream through the wire, the positioning of the components doesn’t matter in this case. The “stream” is being slowed down by the bulbs, and pushed by the batteries, doesn’t matter where. In tug of war for example, it doesn’t matter much where you position the people pulling, as long as they are somewhere on the rope.”
Here the student models electrons as a stream flowing through the wire, extending that model to then say that the positioning of the elements doesn’t matter. They advance this model by saying that the effect of the elements is to push, in the case of batteries, and slow things down, in the case of resistors, and it doesn’t matter where in the “stream” (or the rope, in their tug-of-war analogy) this happens; it just matter that it does.
Both the rank the bulbs explain question and the order of elements explain question provide contexts for eliciting a conceptual model for current as responsive to elements and their order, resistance as limiting current, and voltage as driving current. The order of elements question appears to foreground voltage-as-driver more than the rank the bulbs question, which appears to more frequently cue the resistance-as-limiting resource, at least for the samples of student responses we analyzed.
Mechanical waves questions
 Tension pulse flick question
Tension pulse flick question
The tension pulse flick question gives students two scenarios: one in which a TA creates a pulse by flicking a spring attached to a wall, and the second in which the same TA pulls the spring taut and flicks the spring in the same way, creating a second pulse that propagates down the spring more quickly. The question asks students why it would make sense for a pulse to move faster on a higher-tension spring.
Information for instructors:
The tension pulse flick question is an explain-style question that provides a description of an observation and asks students to say why it makes sense (or doesn’t) to them. The question is a revised version of a question on the Waves Diagnostic Test. Our answer to the tension pulse flick question is that as the spring becomes more taut, the (tension) forces between adjacent parts of the spring increase, such that when one part of the spring is displaced by the disturbance, it pulls the adjacent parts more, and the pulse is propagated down the spring more quickly.
Common ideas and sample student responses:
Student responses to the tension pulse flick question drew on resources that highlighted the ways in which the properties of the medium affect the motion of the pulse, that focused on the up-and-down motion of the spring as the way in which the pulse propagates (and how this motion is affected by changes to the properties of the spring), and that brought in ideas about forces and energy to explain changes in the speed of the pulse. For example:
“The higher the tension of the spring, the more sensitive it is to movement so the pulse can travel faster.”
This student explains that the speed of a pulse depends on the tension in the medium because increased tension means the medium can react more quickly to the pulse. The student goes beyond naming the relationship between tension and pulse speed, toward a nascent causal association.
Other students focused on the forces between parts of the spring, as we did in our answer to the tension pulse flick question. For example:
“When the tension is higher, the particles (or small part[s]) of the springs are pulling each other with more forces. If one particle goes upward, then the particle next to it will be dragged upward. With more forces (= higher tension), it gets dragged even faster (tightly bound). This speed of getting dragged is the speed of the wave, so the higher the tension [the] higher the speed. (c = T/, with same μ.)”
In focusing on a “point,” a “particle,” or a “part” of the spring, this response implies a discretized model of the medium. The student argues that increasing tension makes each particle accelerate more quickly, increasing the wave speed, drawing on reasoning about forces to make sense of pulse propagation.
Students sometimes used reasoning about energy to make sense of faster pulses on higher-tension springs. For example:
“Having a tighter string means less energy gets represented as vertical displacement so that more energy goes into the pulse’s forward movement, i.e., speed.”
In this example, as in many sample textbook solutions that encourage students to break up the energy of a system into its varied forms, the student reasons that in pulse propagation, some energy is in the form of vertical displacement and some in the form of forward movement. When the tension is increased, they reason, the pulse does not go as high, so more energy is able to be “put into” forward movement. Though incorrect, this response associates energy with the shape (“vertical displacement”) of the spring, and associates the speed of the pulse with the tension in the medium, reasoning that energy is associated with or carried by the pulse itself and that energy transfers and transformations play a role in the speed or motion of the pulse.
In general, our experience is that the tension pulse flick question elicits ideas that support student thinking about how propagation happens and why the medium and its properties matter, often drawing on mechanics concepts like force and energy in sense-making.
 Mass density pulse flick question
Mass density pulse flick question
The mass density pulse flick question is very similar to the tension pulse flick question, except the property that is changed between the first and second scenario is the mass density–not the tension–of the spring. In particular, the TA replaces the first spring with a second one that has a higher mass density, and observes that the second pulse moves more slowly down the spring. Students are asked why it would make sense for a pulse to move more slowly down a spring with higher mass density.
Information for instructors:
The mass density pulse flick question, like the tension pulse flick question, is an explain-style question. Our answer to this question is again based on a model in which a pulse propagates by pulling on adjacent parts of the spring. If the tension (and thus the forces between parts) of two springs is the same, but the mass of the parts of one spring is more than the other, the accelerations of the pieces of the more massive spring will be smaller, and the pulse will propagate more slowly.
Common ideas and sample student responses:
As with the tension pulse flick question, student responses to the mass density pulse flick question drew on resources that highlighted the ways in which the properties of the medium affect the motion of the pulse, that focused on the up-and-down motion of the spring as the way in which the pulse propagates (and how this motion is affected by changes to the properties of the spring), and that brought in ideas about forces and energy to explain changes in the speed of the pulse. For example:
“Springs have inertia and heavier springs will have more inertia because inertia is proportional to mass. Since inertia is the tendency to resist change in motion, a heavier spring will oppose the motion of a pulse more.”
This example draws on ideas from mechanics–particularly inertia or a “tendency to resist change in motion”–to make sense of why the speed of the pulse would decrease as the mass density increases.
As in the tension pulse flick question, some students analyzed the spring as a series of discrete chunks, and sense-made about how an increase in mass density would affect the interactions between chunks. For example:
“It would make sense for the pulse to move more slowly on a heavier spring because you could represent each point of mass on the string with a free body diagram and the Fnet on each point of mass is equal to mass times acceleration. (Fnet = ma) Therefore, if the Fnet on each spring is the same as scenario 1, when the mass increases in scenario 2, the acceleration must decrease to compensate. This means that each point on the spring will accelerate more slowly when moving away from the ‘center line’ of the spring, effectively resulting in the pulse moving more slowly.”
This student response closely resembles the answer we offered, adding a reference to the displacement from the spring’s equilibrium.
Also similar to the tension pulse flick question, a number of students performed an energy analysis, splitting the energy among types of movements and reasoning about how changing the mass would affect this split. For example:
“In a heavier spring, there is more mass in a given unit of length. It would take more energy to displace this mass than in a lighter spring. Since more energy is spent on actually displacing the spring in a wave there will be less energy to drive the pulse’s velocity, given that the same amount of energy was applied each time.”
Here, the student reasons that it would take more energy to move a higher-mass chunk (“a given unit of length”). This would leave less energy to “drive the pulse’s” forward movement, and therefore the pulse would propagate more slowly. Though not necessarily canonically correct, this response productively associates energy with the dynamics of pulse propagation.
In our experience, both the tension and mass density pulse flick questions offer an opportunity for students to go beyond understanding that propagation speed is the square root of tension divided by mass density, toward reasoning about how the properties of the medium affect the speed of the pulse. In many cases this reasoning includes modeling the medium as a discrete series of chunks that interact with one another, modeling the pulse as a disturbance that moves these chunks up and down, and drawing on the concepts of forces and energy to explain the dynamics of pulse propagation.
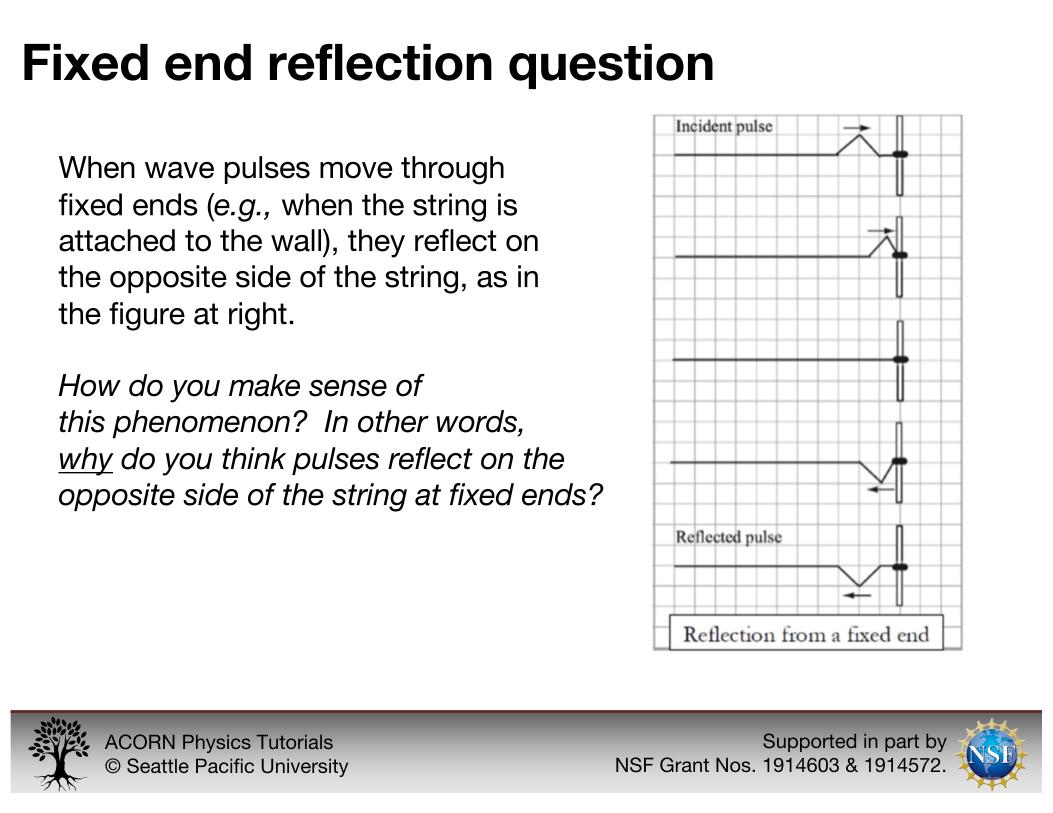
 Fixed end reflection question
Fixed end reflection question
The fixed end reflection question tells students that pulses reflect on the opposite side of the spring at fixed ends, and then asks them why they think that happens.
Information for instructors:
This is an explain-style question. In answering the fixed end reflection question ourselves, at a level that is appropriate for introductory physics students, we analyze the forces on the spring at the fixed end. As the pulse reaches the fixed end, the spring pulls up on the wall, and Newton’s third law tells us that the wall pulls back on the spring, exerting a force downward on the segment of spring that is adjacent to the wall. The downward force from the wall is greater than the upward force from the segment of spring on the other side, the segment closest to the wall accelerates downward and overshoots equilibrium to the other side.
Common ideas and sample student responses:
As we anticipated, students often used the concepts of forces and energy to explain the behavior of pulses at fixed ends, constructing responses with varying degrees of mechanism. For example, one student wrote:
“Every action has an equal and opposite reaction. So as the wave propagates towards the wall, and hits the wall, there is a force upwards on the wall. This means the wall exerts a force downwards on the string. Because F = m(dv/dt) and the wall does not accelerate, the string accelerates downwards, effectively inverting the wave. Also, maybe something to do with energy, ID[on’t]K[now].”
This response applies Newton’s second and third laws to the part of the string near the boundary (the wall), arguing that the pulse is inverted because the string pulls up on the boundary, and the boundary pulls down with an equal and opposite force, which causes the string to accelerate and move past the equilibrium point.
Other students applied energy concepts to reason about reflection on the opposite side of a spring at a fixed end. For example:
“… I believe that the reason it reflects to the other side is due to conservation of energy. Because the wave constantly wants to displace upwards, however [it is] unable to b/c of [the] fixed end. The only way it can go to maintain its energy is to deflect downward. Furthermore, energy has no direction, nor does it care about direction, therefore reflecting downwards does not change the energy state.”
Here, the student argues that conservation of energy requires that a pulse continue (it can’t just disappear), and since it can’t keep going up at the fixed end, it has to “deflect downward.” They add that because energy doesn’t have a directionality (only a magnitude), the top and bottom of the spring are effectively the same.
Some responses to the fixed end reflection question used procedures–such as modeling the reflected pulse as the superposition of the “incoming” pulse and an inverted “ghost” pulse–but this was less common than responses that drew on concepts of forces, motion, and energy to explain why the reflected pulse was on the opposite side of the spring. This suggests to us that the fixed end reflection question may support students in bridging ideas from mechanics to sensemake about fundamental pulse reflection phenomena.
 Superposition mechanism question
Superposition mechanism question
Like the tension pulse flick question, the mass density pulse flick question, and the fixed end reflection question, the superposition mechanism question is an explain-style question that describes a fundamental wave mechanics scenario and asks students why they think it happens that way. In particular, the superposition mechanism question tells students that when two pulses on the same side of a spring meet, they add–an example of superposition. They are then asked why pulses add when they are on the same side of the spring, or why superposition works the way it does.
Information for instructors:
Our hope was that students would go beyond restating the principle of superposition (mathematically or conceptually) and instead draw on mechanics principles to sensemake about the phenomenon. Our answer to the superposition mechanism question is that the leading edge of each pulse pulls upward on the segment of spring between them just before they meet. The force by each leading edge on this “middle segment” is determined by the tension in the spring and the shape of each pulse (sharper pulse means higher force). This means the “middle segment” accelerates in a way that is determined by the sum of the forces delivered by each leading edge. This kind of logic can be extended to the entire time period that the pulses overlap, leading to the same conclusions that the mathematical principle of superposition does.
Common ideas and sample student responses:
As we had hoped, students did draw on mechanics concepts–particularly forces, energy, speed, and acceleration–to explain why pulses add when they are on the same side of the spring.
“If the strings are both accelerating up, they will both accelerate up with twice the force.”
This response makes sense of superposition using the acceleration of parts of the spring. When two pulses that are both accelerating the spring up superpose, the string then “accelerate[s] up with twice the force,” making the string move even higher.
Another student responded using imagery of free body diagrams, writing:
“Imagine that the two pulses are forces acting upon an object in the same direction. [Drawing of box with two arrows whose tails are on the right side of the box and heads are pointing horizontally outward from there.] The total force on the object would be the sum of these two forces (constructive interference).”
Here, the student analogizes constructive interference to a sum of forces, where the spring is the object and the pulses are forces. When the forces are in the same direction, the spring experiences a net force that is the sum of those two forces, displacing it further.
Yet other students used energy to sensemake about superposition. For example, one student wrote:
“This principle is in line with the conservation of energy, if they weren’t added together, energy in the wave would be lost.”
While this response isn’t as clearly mechanistic (to us) as responses that draw on acceleration and forces, it does associate energy with the amplitude of the pulse, and uses conservation rules to sensemake about why the pulses can’t just disappear.
Some students also drew on resources for reasoning about what a pulse is, arguing that pulses superpose because they can occupy the same space at the same time (in contrast to, say, discrete objects).
“Superposition works because waves can occupy the same space at a given time therefore the net wave is the sum of the waves. Since the waves are on the same side, their displacements are (in this case) ‘positive’ and we add the pulses.”
These responses are less obviously about what makes pulses add when they are on the same side of the spring and are more clearly about what it is about pulses that makes it possible for them to add in the first place. This ontological characterization of pulses as not-objects challenges some of the findings from misconceptions-oriented studies of student understandings of waves, suggesting that the extent to which students think of pulses as objects depends on the context (Robertson et al. 2019).
In short, the superposition mechanism question, like the other waves questions we’ve offered here, may be especially appropriate for supporting connections between mechanics ideas and wave dynamics, and (in this case) for eliciting ideas about the nature of pulses as displacements of the spring that can co-occupy space.
Heat and temperature questions
 Metal blocks question
Metal blocks question
The metal blocks question tells students that two metal blocks sitting on a table, one hot and one cold, are placed in contact with one another, and that over the next several minutes, the blocks become the same temperature as one another, and eventually the same temperature as the room. The question asks students what mental model helps them explain why this happens.
Information for instructors:
The metal blocks question is an explain-style question that asks students to apply a model to explain why we observe the behavior described in the question. Our own answer to this question is temperature changes happen when thermal energy moves into or out of an object. When two objects at different temperatures come into contact (such as the two blocks, one hot and one cold, or the hot block and the room), thermal energy transfers until the two objects are the same temperature. (This equilibrium-seeking could be explained in terms of entropy, micro- and macrostates, collisions between particles at the surface of the object, etc.)
Common ideas and sample student responses:
Students used a variety of resources in their responses to this question, including highlighting that temperature changes as a result of thermal energy transfer, naming properties that affect temperature change or thermal energy transfer (e.g., temperature difference, mass or material of objects), citing the Second Law of Thermodynamics, identifying collisions between particles as a mechanism for energy transfer, and evoking a model of a reservoir to explain undetectable changes in temperature (such as in the environment).
For example, one student wrote:
“Heat flows from hot environments to colder environments. So I would think as soon as the cold block touched the hot block heat was transferred to it, and heat from the hot block was being released to the environment via heat waves. So as the heat that is being transferred into the cold block, as soon as the heat enters the cold block it is also emitted into the environment.”
This response draws on a number of resources for understanding thermal phenomena, including the Second Law of Thermodynamics, the idea that thermal energy transfers at contact, and the awareness that multiple objects at different temperature are in contact.
Some students articulated a mechanism for thermal energy transfer at contact. For example:
“There is a transfer of kinetic energy between fast moving molecules (in the hot block) with slow moving molecules (in the cold block). Which facilitates the transfer of having both blocks being the same temperature.”
Here, the student articulates that particles in the hot block will be moving faster than particles in the cold block, such that when the two come into contact, energy will transfer between them.
Students also referenced diffusion and reservoirs, for example:
“The concept of diffusion, hot air will travel to the cold and cold to hot until it reaches equilibrium. The heat in both block will reach back and forth but the room is way bigger, the heat from both block will expand towards the room, but the size of the room is way bigger, both hot and cold waves of temperature would just decrease and increase until it is at an equilibrium with the room temperature.”
This student paints an image of thermal energy exchange and movement through space, where energy travels between objects until equilibrium is reached. They justify the stable temperature of the room in terms of it being big, like a reservoir where thermal energy can spread out such that the temperature change of any one part is negligible.
In the metal blocks question, as with other thermal physics questions we asked, elicited a variety of resources, many of which blended everyday and physics classroom language to predict or explain thermal phenomena. The metal blocks question in particular appears to foreground energy transfers at contact, and equilibrium-seeking, alongside some mechanisms for both.
 Heat transfers from hot to cold question
Heat transfers from hot to cold question
The heat transfers from hot to cold question cites a colloquial version of the Second Law of Thermodynamics – that heat or thermal energy transfers from hot to cold – and asks students how they make sense of this.
Information for instructors:
The format of this is an explain-style question, but the content is somewhat different; rather than asking students to explain the observed behavior of a system, we ask them to say how they make sense of a “rule” they have learned in physics class.
There are a variety of canonically correct answers to this question. Our answer focuses on the microscopic processes: microscopically, hot objects have higher temperatures, which corresponds to particles with higher kinetic energy. When two objects come into contact, one hot and one cold, the interactions between the higher—and lower—energy particles at the point of contact transfer some of the energy to the colder object.
Common ideas and sample student responses:
Students used a variety of resources in their responses to this question. Some responses were tautological–e.g., thermal energy transfers from hot to cold because that’s what thermal energy does–but many responses gave us insight into how students are thinking about thermal energy, equilibrium, and entropy.
Several student responses mimic our microscopic analysis. For example:
“Thermal energy is a result of the movement of the particles so there is no way you could transfer no movement, so the only direction is transferring movement to no movement.”
Though this student is incorrect in suggesting that colder objects have no particle movement at all, this response does name a mechanism for the directionality of thermal energy transfer: collisions between particles moving at different speeds.
Other student responses gave us insight about how they might be thinking about equilibrium (and thus what kinds of activities or analogies might support continued conceptual development). For example, one student wrote:
“Heat transfers from hot items to cold items because of the universe’s ‘need’ for balance. Equilibrium is the most stable state for the universe to be in and that is seen in exchange of heat as well. The hot item’s molecules have more kinetic energy than the molecules of the cold items. Energy can be shared as heat so in order for the two objects to have equal energies, heat flows from the object with higher energy to the object with lower energy.”
This response personifies the universe as having a need for balance and stability, saying that transferring energy from the hot object (whose molecules have more kinetic energy) to the cold one creates the conditions under which the two objects can have equal energies. Other responses referenced “evening out,” “concentration,” and “spreading out.”
Still other responses directly referred to entropy and micro- or macrostates, though these responses were less common. For example:
“Thermal energy transfers from hot to cold objects, and not the other way around because of entropy. Since entropy cannot decrease in a closed system, the system tends toward high entropy. One object having higher temperature than another is a more organized state than both objects being in thermal equilibrium, so thermal energy tends to transfer from hot objects to cold objects.”
This response cites a colloquial definition of entropy as being about the degree of organization of a particular state, saying that the state in which more energy resides in one object is more organized than the state in which objects share the energy equally, and thus the tendency is toward the latter.
In short, the heat transfers from hot to cold question appears to do what it was designed to do, which is to support us (instructors and researchers) in better understanding how students are thinking about the nature of thermal energy transfer, equilibrium, and entropy.
 Particles and cubes what-is-possible questions
Particles and cubes what-is-possible questions
The particles and cubes what-is-possible questions ask students what scenarios are possible as a result of given experimental set-ups. These are explain-style questions that are meant to explore student thinking about statistical probability.
Information for instructors:
Correct answers to the what-is-possible questions depend on the assumptions students make. For example, if three identical cubes are left in boiling water for 5 minutes before their temperatures are measured, the final measured temperature possibilities may differ based on whether the student assumes the cubes have a small number of particles in them or a large (N ~ NA) number of particles. The second law of thermodynamics states that entropy does not decrease, which in tangible terms means that heat flows from hot to cold. For a cube system with a small number of particles, it is possible, however unlikely, for the cubes to end up with slightly different temperatures. The larger the system (or the larger the number of particles), the less likely the system is to stray from equilibrium. The 3 particle system has a higher likelihood of being “off-balance” (having particles with different speeds) than the 3-cube system (where “off-balance” would be defined as having different temperatures).
Common ideas and sample student responses:
This set of questions elicited both conceptual and epistemological resources. We saw a mix of resources related to both probability and predictability. One student stated (in response to “cubes”):
“This doesn't make sense, as temperature wants to equalize, and the water would have to drain energy from one of the cubes, violating the second law of thermodynamics.”
This student demonstrates an understanding that that equilibrium is the most probable state (”temperature wants to equalize”). They also state that the outcome proposed in the question is not possible due to physics laws (”the water would have to drain energy […] violating the second law”), which we interpret as pointing to the student’s thinking about how we know in physics (epistemology).
(In response to “cubes”): “In theory, the energy in the system has the highest probability of being distributed equally to all of the cubes, thus heating them all equally. However, in practice, it is possible for more energy to enter one of the cubes than the others, thus explaining this situation.”
This student uses the resource that energy and temperature are related (”energy […] being distributed equally […] thus heating them all equally”); they also state that the stated outcome is possible, due to the random behavior of particles, but unlikely (”in theory […] highest probability of being distributed equally […] in practice, it is possible for more energy to enter one […] than the others”).
(In response to “particles”): “No, since particles collide elastically, so since all three particles initially had the same speed, they will maintain the same speed.”
This response uses multiple relevant ideas, such as the idea that identical experiments will have identical outcomes (”all three particles initially had the same speed, they will maintain”), an idea more closely tied to predictability than probability. They also draw on the resource that energy and speed are related, but particularly attend to collisions as a mechanism for energy transfer, pointing out that because the collisions are elastic, there is no transfer of energy and therefore no change in speed. (”particles collide elastically, so […] they will maintain the same speed”).
The types of ideas students used in their responses covered a wide range. More importantly, it sheds relevant light on how students think about the possibility of scenarios occurring, and the context-dependence (microscopic particles vs. macroscopic cubes) of their ideas, reasoning, and beliefs about physics.
People
Current Team Members
 |
Amy Robertson (she/her, PI, Seattle Pacific University) is a Research Professor and physics education researcher with a strong interest in cultivating liberatory classroom and professional spaces. In her work, Amy roots herself in a variety of methodological tools, disciplinary and interdisciplinary collaborations, and her lived experience as a disabled and chronically ill physicist. Her research focuses on university students’ conceptual resources for learning physics and how frameworks from equity and justice can help physicists become more critically conscious. She is a proud puppy mama, a disabled hiker, and an avid crafter. |
 |
Paula Heron (she/her, PI, University of Washington) is a Professor of Physics at the University of Washington. She has been engaged in physics education research with a focus on improving student conceptual understanding and reasoning ability for nearly 30 years. She is involved in a number of international organizations and collaborations in PER and has been recognized by awards from the American Physical Society and the American Association of Physics Teachers. Dr. Heron is an Associate Editor of Physical Review Physics Education Research. |
 |
Rachel Scherr (she/her, co-PI, University of Washington) is an Assistant Professor of Physics at the University of Washington Bothell. A longtime physics education researcher, she has a special interest in educator development, including physics faculty, K-12 teachers, graduate teaching assistants, and undergraduate learning assistants. Dr. Scherr is the producer of Periscope Video Lessons. |
| Raphael Mondesir (he/his, co-PI, Seattle Pacific University) is an Assistant Professor of Sociology at Seattle Pacific University. As a quantitative sociologist, Dr. Mondesir utilizes a variety of methods to study the intersection of community development, civic participation, and religious pluralism in the Global South. His special interest in civic cultures and social networks often inform his teaching and how he builds relationships with his students. Dr. Mondesir spends his weekends playing soccer or hiking. | |
 |
Lisa Goodhew (she/her) is an Assistant Professor of Physics at Seattle Pacific University. Her research focuses on university students’ conceptual resources for understanding physics and supporting instructors in effectively leveraging these resources. Dr. Goodhew’s favorite part of her work is getting to know and learn with students in and out of the physics classroom, and she is excited by the ways this research makes her a better teacher. |
 |
Lauren Bauman (she/her) is a research coordinator at the University of Washington Seattle. She first became interested in physics education research while learning physics as an undergraduate and is particularly interested in effectively creating empowering, equitable, and supportive educational spaces that authentically center students' ideas. Most of her research focuses on analyzing written data to identify students' conceptual resources. |
 |
Anne Alesandrini (they/them and she/her) is a current graduate student with the Physics Education Group at the University of Washington and a former public high school teacher. Their research interests include student explanations and educator development, and they spend a lot of time thinking about the interactions between education, science, and society. They find joy wandering around outside with their kids looking at plants. |
 |
Al Snow (they/them) is a graduate student in Physics at the University of Washington. They are currently working on classroom discussion video analysis and pretest response analysis. Al enjoys reading and writing, as well as listening to and performing music. |
 |
Sam McKagan (she/her) is the creator and director of PhysPort, a website that supports physics faculty in research-based teaching and hosts open-source curricular materials, including the ACORN Tutorials. She has conducted research into physics faculty members’ and department heads’ needs around research-based teaching and assessment, and conducted several meta-analyses of the impact of research-based teaching in physics. For this project, Sam worked with Adrian to design the ACORNS Tutorials website on PhysPort, and helped analyze interviews with faculty. |
 |
Adrian Madsen (she/her) is the assistant director of PhysPort, a website that supports physics faculty in research-based teaching and hosts open-source curricular materials, including the ACORN Tutorials. She has conducted research into physics faculty members’ and department heads’ needs around research-based teaching and assessment, and conducted several meta-analyses of the impact of research-based teaching in physics. For this project, Adrian worked with Sam to design the ACORNS Tutorials website on PhysPort, and helped analyze interviews with faculty. |
Team Alumni
 |
Yohannes M. Abraham (he/him) is a former undergraduate cellular and molecular biology student at Seattle Pacific University interested in STEM teaching and learning as well as the medical field. He joined physics research to better understand why students’ have common conceptual misconceptions about physics and how to address these difficulties with a resource-oriented teaching and learning approach. He plans to work in a biology laboratory and wishes to attend medical school in the future. During his free time, he loves to play soccer, try different cuisines, and read Italian classic books. |
| Cheyenne Broadfoot is a graduate from University of Washington Bothell with a B.S. in Physics and is currently pursuing a M.S. in Coastal Zone Management and Marine Conservation from University of Miami Rosenstiel School of Marine and Atmospheric Science. She has a passion for learning and wants to use the acquired knowledge to work for an organization addressing wastewater and pollution in third world countries, specifically Costa Rica. | |
 |
Beth Gallatin is a former undergraduate student at South Puget Sound Community College studying computer science. She joined the physics education research project to help develop a deeper understanding of students' conceptual resources and begin exploring strategies to create a more inclusive and diverse society of physicists. She is currently participating in research for the LIGO Collaboration working on the search for continuous wave gravitational radiation. She loves thinking and wondering about gravity, and the role it plays in our understanding of the universe. She has a persistently curious mind, and plans to focus on a career that bridges scientific resources, nature, and humanity. |
 |
Jon Geiger is a graduate of Seattle Pacific University, where he received degrees in Physics, Applied Mathematics, and Honors Liberal Arts. He served as a Learning Assistant for three years, and has worked with the team on a project investigating the utility of natural language processing in characterizing students’ conceptual resources in physics. |
 |
Brynna Hansen is a former undergraduate student studying Cellular and Molecular Biology at Seattle Pacific University, and does physics education research as a side hobby! She hopes to attend medical school following graduation. Outside of school Brynna loves to read, exercise and spend time with loved ones. |
 |
Tra Huynh (she/her) is a former postdoctoral scholar at University of Washington Bothell. She is a physics education researcher and she has been conducting qualitative research on faculty and student professional development and equity education through multiple lenses of methodology and theories. She loves creating ideas with people and turning them into research. She is an aspiring knitter and baker. |
 |
Katie Marvin is a graduate of UW Bothell with a BS in physics. Before becoming a student, she was a dog trainer who taught large classes to the general public. Her experience in behavioral training, communication, and observation served her well as she worked her way through an associate's degree at South Seattle College. These same skills would prove useful when she was encouraged to join the physics education research project for her independent research credits. She has a passion for learning, teaching, and bringing out the best in others. After graduating she landed a job within the semiconductor industry. She plans to become a physics instructor someday after she has gained some real world application experience. With the free time she has, she likes to practice her woodwind instruments, hike, play retro games, and hang out with her dog, Zac. |
 |
Clausell Mathis is a former postdoctoral scholar in physics at the University of Washington - Seattle. Clausell has been engaging in physics education research over the past 4 years with a focus on understanding how physics instructors can incorporate culture-based equitable approaches to teaching from a curriculum development, student learning, and teacher identity lens. |
 |
Jon Owen (he/him) is a former undergraduate student in physics at Seattle Pacific University. He is works to analyze videos of classrooms using ACORN Physics tutorials to understand how students’ conceptual resources are activated and refined. |
|
Olin Sorby is a former Undergraduate student studying Applied Physics and Norwegian language at the University of Washington. He worked with Tra on identifying conceptual resources in kinematics, pertaining to productive use of force reasoning in kinematics problems. |
|
 |
Marcella Su (she/her) is a graduate of the University of Washington Bothell with a B.S in Biochemistry and a minor in Health Studies. She is pursuing medicine to become a doctor. She believes that research is essential to medicine in order to propel the field of medicine to create effective treatments for the members of our community. She hopes to practice and provide quality care for her community after medical school, as closing the gap between ethnic and marginalized groups is a core passion of hers. She is currently a Research Assistant at Veterans Affairs, Seattle Epidemiologic Research and Information Center. During her time off she helps her family in residential housing management, volunteers at International District Emergency Center, located in Seattle’s Chinatown, and does sewing with a sewing machine to help tailor clothing for family and friends. |
 |
Andrea Wooley (she/her) is a former undergraduate physics student at Western Washington University with experience in physics education research and Mossbauer spectroscopy. The culture of physics is central to her research interests, in particular she is passionate about issues about justice, equity, inclusion and diversity. She’s a transfer student from South Seattle College where she studied students’ perspectives of physics in addition to working as a tutor and peer navigator. She spends her weekends hiking in Larabee state park, playing pool and taking care of her house rabbit, Monty. |
Research
ACORN Physics Tutorials are developed iteratively, in conversation with research:
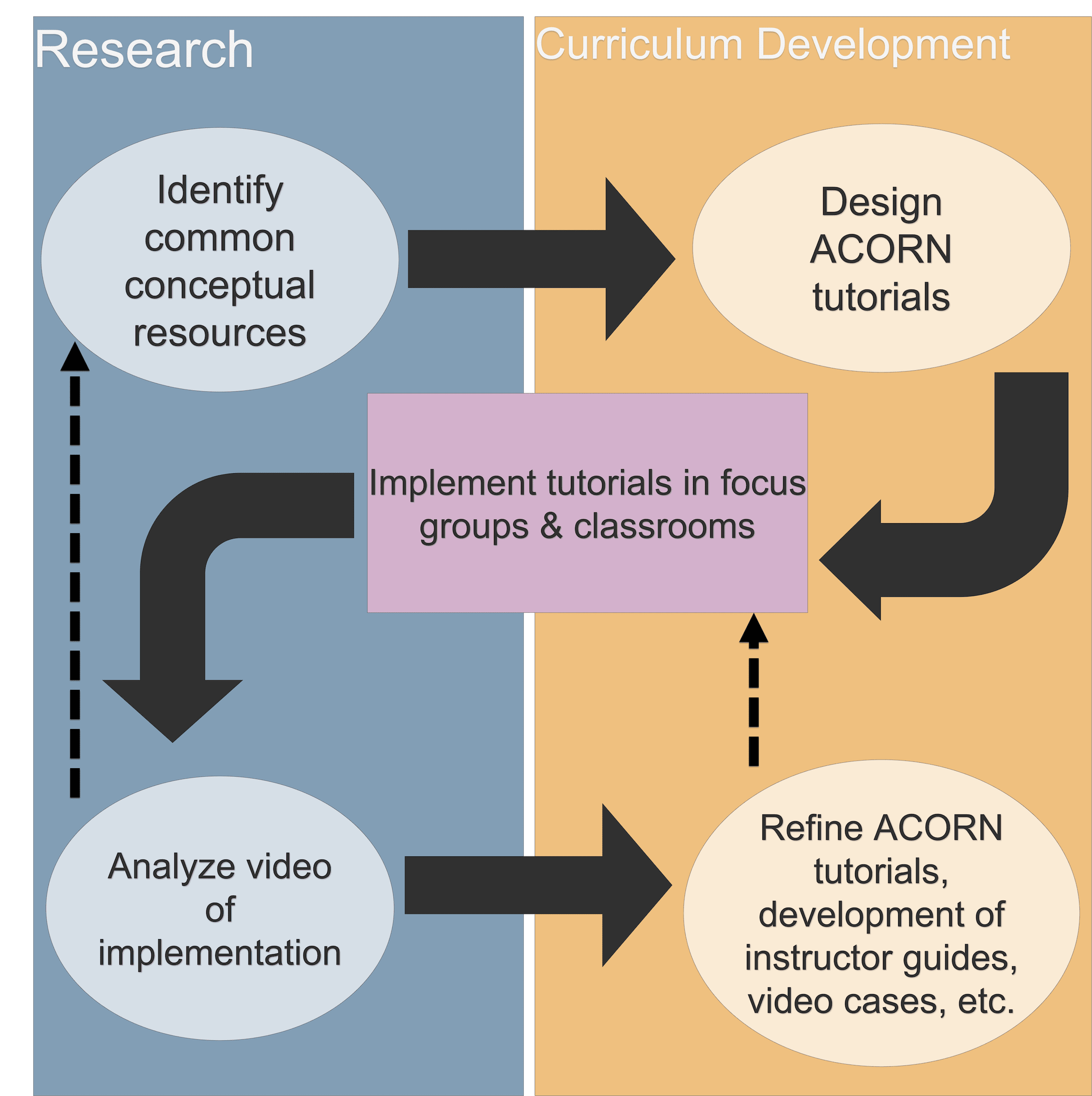
Researchers from our team first use student written responses to conceptual questions to identify specific, common conceptual resources for understanding a particular topic. This research shapes the initial design of an ACORN Physics Tutorial, which elicits and then builds from identified conceptual resources, toward models, mechanisms, and concepts. These tutorials are then implemented in focus groups or classrooms, where students are video-recorded as they learn. Video analysis identifies ways in which the tutorial is working or not working as planned – or working well in unexpected ways – and this analysis then shapes the refinement of the materials. Often materials iterate through this process multiple times before being shared more broadly.
Research identifying students’ conceptual resources for understanding physics
Kinematics
- T. Huynh, A. Alesandrini, L. Bauman, O. Sorby, and A. Robertson, Drawing on force ideas for kinematic reasoning in introductory physics, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- C. Broadfoot, B. Hansen, A. Robertson, and L. Goodhew, Identifying student resources for understanding kinematics, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
Forces
- T. Huynh, A. Alesandrini, L. Bauman, O. Sorby, and A. Robertson, Drawing on force ideas for kinematic reasoning in introductory physics, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- A. Robertson, L. Goodhew, R. Scherr, and P. Heron, University student conceptual resources for understanding forces, Phys. Rev. Phys. Educ. Res. 17 (1), 010121 (2021).
Linear Momentum
- B. Hansen, L. Bauman, Y. Abraham, M. Valentin, and A. Robertson, Identifying student resources for understanding linear momentum, presented at the Physics Education Research Conference 2021, Virtual Conference, 2021.
Energy
- H. Sabo, L. Goodhew, and A. Robertson, University student conceptual resources for understanding energy, Phys. Rev. Phys. Educ. Res. 12 (1), 010126 (2016).
Circuits
- L. Bauman, T. Huynh, and A. Robertson, Substance-based and sequential reasoning about current: An example from a bulb-ranking task using a resources theoretical lens, Phys. Rev. Phys. Educ. Res. 20 (1) 010124 (2024).
- L. Bauman, B. Hansen, L. Goodhew, and A. Robertson, Student conceptual resources for understanding electric circuits, Phys. Rev. Phys. Educ. Res. 20 (2) 020128 (2024).
- L. Bauman, J. Corcoran, L. Goodhew, and A. Robertson, Identifying student conceptual resources for understanding electric current, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
Waves
- L. Bauman, L. Goodhew, and A. Robertson, Students’ use of conceptual resources for understanding superposition, presented at the Physics Education Research Conference 2019, Provo, UT, 2019.
- L. Goodhew, A. Robertson, P. Heron, and R. Scherr, Student conceptual resources for understanding mechanical wave propagation, Phys. Rev. Phys. Educ. Res. 15 (2), 020127 (2019).
- A. Robertson, L. Goodhew, P. Heron, and R. Scherr, Pulses as not-objects: student responses to a new question about the superposition of mechanical waves, Phys. Educ. 54 (5), 055023 (2019).
Heat and Temperature
- A. Alesandrini, T. Huynh, L. Bauman, and A. Robertson, Identifying student resources for reasoning microscopically about heat and temperature, presented at the Physics Education Research Conference 2022, Grand Rapids, MI, 2022.
- Y. Abraham, M. Valentin, B. Hansen, L. Bauman, and A. Robertson, Exploring student conceptual resources about heat and temperature, presented at the Physics Education Research Conference 2021, Virtual Conference, 2021.
Research analyzing implementation of ACORN Tutorials
- L. Bauman, L. Goodhew, A. Alesandrini, A. Snow, and A. Robertson, Shifts in students’ responses to conceptual questions after a new physics conceptual worksheet: Preliminary findings, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- A. Robertson, L. Bauman, Y. Abraham, B. Hansen, H. Tran, and L. Goodhew, Resources-oriented instruction: What does it mean, and what might it look like?, Am. J. Phys. 90 (7), 529 (2022).
- L. Goodhew, A. Robertson, and P. Heron, A case of resources-oriented instruction in calculus-based introductory physics, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
Related research by the development team
- J. Owen, L. Goodhew, and B. Hansen, "Which has more energy?" - An example of responsive teaching in university physics, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- A. Robertson, L. Goodhew, L. Bauman, B. Hansen, and A. Alesandrini, Identifying student conceptual resources for understanding physics: A practical guide for researchers, Phys. Rev. Phys. Educ. Res. 19 (2), 020138 (2023).
- A. Snow, P. Heron, L. Bauman, A. Robertson, and L. Goodhew, A case in which canonically incorrect ideas do not hinder conceptual progress in introductory physics, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- J. Geiger, L. Goodhew, and T. Odden, Developing a natural language processing approach for analyzing student ideas in calculus-based introductory physics, presented at the Physics Education Research Conference 2022, Grand Rapids, MI, 2022.
- A. Robertson, L. Goodhew, P. Heron, and R. Scherr, Impetus-Force-Like Drawings May Be Less Common Than You Think, Phys. Teach. 60 (4), 254 (2022).
- L. Bauman, C. Mathis, S. McKagan, A. Madsen, K. Marvin, L. Goodhew, and A. Robertson, Centering physics faculty ideas about resources-oriented instruction, presented at the Physics Education Research Conference 2021, Virtual Conference, 2021.
- L. Goodhew, A. Robertson, P. Heron, and R. Scherr, Students’ context-sensitive use of conceptual resources: A pattern across different styles of question about mechanical waves, Phys. Rev. Phys. Educ. Res. 17 (1), 010137 (2021).
- A. Robertson, L. Goodhew, R. Scherr, and P. Heron, Impetus-Like Reasoning as Continuous with Newtonian Physics, Phys. Teach. 59 (3), 185 (2021).
- R. Mondesir and A. Robertson, Toward characterizing the demographics of introductory physics courses, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
- L. Goodhew, A. Robertson, P. Heron, and R. Scherr, Examining the productiveness of student resources in a problem-solving interview, presented at the Physics Education Research Conference 2018, Washington, DC, 2018.
What are ACORN Physics Tutorials?
- Designed to support learning environments that Attend to Conceptual Resources in Physics. Conceptual resources are “seeds of science” that can grow toward sophisticated understandings with support and cultivation.
- Based on research about student thinking in introductory physics classrooms.
- Meant to support sense-making about forces, mechanical waves, circuits, linear momentum, kinematics, and heat and temperature.
- Supplemented by instructor guides, classroom video cases, and research that can inform and support implementation.
Why use ACORN Physics Tutorials?
- To enact instruction that treats students as having good ideas that can serve as the basis for instruction.
- ACORN Physics Tutorials reliably elicit specific conceptual resources among students in our instructional contexts.
- We support you in noticing student resources as they come up and deciding what you might do next.
- To help your students engage in the disciplinary practice of sense-making about science, as they develop conceptual understandings of forces, mechanical waves, circuits, linear momentum, kinematics, and heat and temperature.
Topics
What's Included
- Worksheets for use in your classes
- Instructor guides
- Classroom video cases
- Materials for a pedagogy course for TAs and LAs