Tutorial details

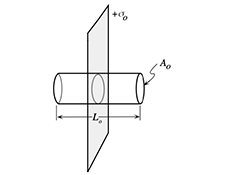
In the first part of the tutorial, students are introduced to the idea of a Gaussian surface. They first consider the flux through each part of a Gaussian cylinder (the two end caps and the curved side) and determine the sign of the net flux through the cylinder for three cases: a uniform field, and two different arrangements of point charges. Students then consider a fourth case in which it is not possible to determine the sign of the net flux with previously developed concepts. (A point charge outside the cylinder.) This motivates the introduction of Gauss’ law in the second section of the tutorial. At this point, students are asked to check their answers with a tutorial instructor. The third case, in which two oppositely charged point charges are placed on the axis of the cylinder, requires a symmetry argument, which is challenging for most students. It may be helpful to ask students to consider the behavior of the cosine function around 90 degrees [i.e., cos(90+θ) = cos(90–θ)].

In the second section of the tutorial, students are introduced to Gauss’ law and revisit the cases considered in section I. They then apply Gauss’ law to find the flux through several Gaussian surfaces for various arrangements of point charges.

In section III, students apply Gauss’ law to find the flux through a cylinder that encloses a section of an infinite sheet of charge. They use the relationship between flux and electric field to find an expression for the magnitude of the electric field near the center of a large sheet of charge. At this point, students are again asked to check their answers with a tutorial instructor. Many struggle with the idea that the electric field due to a sheet of charge does not depend on the distance from the sheet. At the end of the tutorial, students use Gauss’ law to find the electric field due to two parallel sheets of charge, and compare their results using this method to the results obtained using superposition.

For instruction tips, login or register as a verified educator to see the Instructor Guide.

Prerequisite tutorials

The Electric fields and flux tutorial is a prerequisite to Gauss' law.

Other prerequisites

This tutorial builds directly on Electric fields and flux. Familiarity with area vectors, electric field, electric field lines, and electric flux is assumed. Students must also be familiar with the definition of charge density, the distribution of charge on conductors, and the electric field inside a conductor. No knowledge of Gaussian surfaces or of Gauss’ law is assumed.

Equipment

List

• white board or large sheet of paper with markers

Discussion