Effect size: What is it and when and how should I use it?
Introduction to effect size:
When making changes in the way we teach our physics classes, we often want to measure the impact of these changes on our students' learning. Often we do this by administering a research-based assessment at the beginning and end of the class and calculating the change between pre and post. There are several different measures that can be used to tell you, in one number, how to compare learning in different courses and using similar measures. In the physics education research community, we often use the normalized gain. In social sciences research outside of physics, it is more common to report an effect size than a gain. An effect size is a measure of how important a difference is: large effect sizes mean the difference is important; small effect sizes mean the difference is unimportant. It normalizes the average raw gain in a population by the standard deviation in individuals’ raw scores, giving you a measure of how substantially the pre- and post-test scores differ.
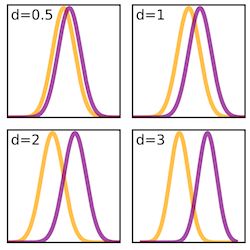
Effect size is calculated using Cohen’s d, which is found using the following formula:
d = (<post>-<pre>)/stdev
There are suggested values for small (.2), medium (.5), and large (.8) effect sizes. Those values and their labels are treated as meaningfully different. Here, 'stdev' is the pooled standard deviation of the pre- and post-test scores and <post> and <pre> are the class average pre- and post-test scores. Effect size is calculated only for matched students who took both the pre-test and the post-test.
Effect size is not the same as statistical significance: significance tells how likely it is that a result is due to chance, and effect size tells you how important the result is. In a statement on statistical significance and P-values, the American Statistical Association explains, "Statistical significance is not equivalent to scientific, human, or economic significance. Smaller p-values do not necessarily imply the presence of larger or more important effects, and larger p-values do not imply a lack of importance or even lack of effect. Any effect, no matter how tiny, can produce a small p-value if the sample size or measurement precision is high enough, and large effects may produce unimpressive p-values if the sample size is small or measurements are imprecise. Similarly, identical estimated effects will have different p-values if the precision of the estimates differs."
When should I use effect size?
You can look at the effect size when comparing any two assessment results to see how substantially different they are. For example, you could look at the effect size of the difference between your pre- and post-test to learn about how substantially your students knowledge of the subject tested changed as a result of your course.
Advantages of effect size
Because the standard deviation includes how many students you have, using the effect size allows you to compare teaching effectiveness between classes of different sizes more fairly. Effect size is a popular measure among education researchers and statisticians for this reason.
In social sciences research outside of physics, it is more common to report an effect size than a gain. By using effect size to discuss your course, you will better be able to speak across disciplines and with your administrators.
Differences between effect size and normalized gain
The major mathematical difference between normalized gain and effect size is that normalized gain does not account for the size of the class or the variation in students within the class, but effect size does. By accounting for the variance in individuals' scores, effect size is a lot more sensitive single number measure than the normalized gain. The difference is more pronounced in very small or diverse classes. Because error usually decreased with increasing sample size, small classes are a lot more vulnerable in normalized gain than they are in effect size: the same teaching year after year can make wild swings in normalized gain, but smaller changes in effect size.
Normalized gain helps account for the effect of differing pre-test levels, which allows us to compare courses with very different pre-test scores. Effect size helps account for the effect of differing sizes of error, which allows us to compare courses with different levels of diversity in scores and class sizes. It is statistically more robust to do the latter.
Normalized gain fulfills all the cultural functions of effect size within the PER community, as it is a single number which helps you understand the effectiveness of your teaching, and can be compared to a standard range of values.
The ranges for small (~.2) medium (~.5), and large (~.8) effect sizes are different than those for normalized gain: small (<.3, "trad range"), medium (.3 to .6, "IE range"), and large (>.7). Unlike normalized gain, effect size has no upper boundary, though effect sizes are generally less than 2.
| Size | Effect size | Example (from Cohen 1969) |
| 'Large' | 0.8 | difference between heights of 13- and 18-year-old girls in the US |
| ‘Medium’ | 0.5 | difference between heights of 14- and 18-year-old girls in the US |
| ‘Small’ | 0.2 | difference between heights of 15- and 16-year-old girls in the US |
 Add a Comment
Add a Comment


