SCALE-UP
What does it look like?


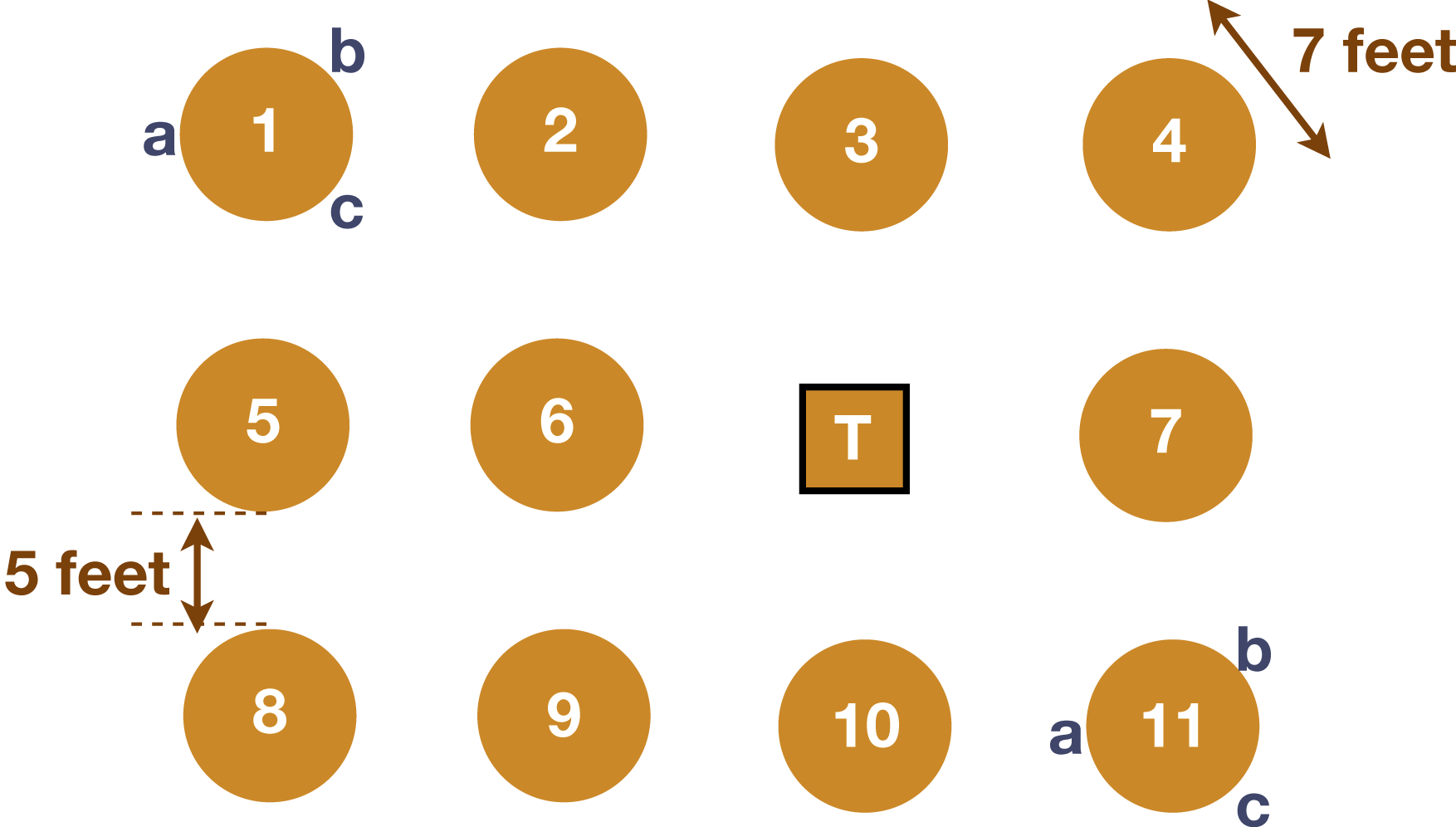
SCALE-UP is not a curriculum, but a physical classroom structure that encourages student interaction and discourages instructor lecturing. SCALE-UP classrooms often look more like a restaurant than a lecture hall. Students sit at special tables that each seat three groups of three students*, and there is no front of the classroom. Students have access to whiteboards, computers, internet, and lab equipment, and technology may allow the instructor to project student work onto screens around the room. There is no separate lecture, lab, and recitation; all of these activities are integrated into one setting. While there is no specific curriculum for SCALE-UP, activities should emphasize conceptual understanding and students working together. Having multiple groups at a table encourages students to interact not only within their groups, but also with other groups. Students are expected to read and master basic material before coming to class, so they spend class time working through problems rather than absorbing information. Students are trained to work effectively in groups, and are often assigned group roles to facilitate participation. Instructors monitor student understanding throughout class, and can flexibly change the pace or direction of class accordingly.
*There are also many variations of this arrangement, such as round, D-shaped or trapezoidal tables, with different numbers of groups and/or students at a table. For more details on variations, see Adapting to other environments.
Classroom Video
SCALE-UP/TILE at the University of Iowa:
Sample Materials
Below are some sample activities for SCALE-UP. You can find many more in the teaching materials section.
Examples of “Tangible” Activities
- “Find the thickness of a single page from your textbook. Use this result to find the diameter of a period at the end of a sentence in the book.” Students invariably start by dividing the estimated or measured thickness of a large stack of the pages by the number of sheets of paper in the stack. Although they usually don’t think of it in these terms until prompted, the reason for using many sheets at once is to increase the number of significant digits in the final answer. In a Socratic dialog, students are asked questions about why they tackled the problem as they did. (This is often done by having them consider what answers they would have gotten from a different approach). By recognizing for themselves how significant figures play a role in measurement, they are much more likely to continue to consider the uncertainty in their measurements throughout the course.
- “Find the coefficient of kinetic friction between your book and the table.” Here the students slide their books across the table, estimating initial velocity and measuring stopping distance.
- “Determine the angular acceleration of a rotating racquetball as it spins to a stop on your table.” or “What is the impulse that the floor applies to a bouncing racquetball?” These types of very brief activities help students build an intuitive understanding of otherwise abstract concepts.
- “Find the number of excess charges on a piece of tape pulled off the table.” This exercise, adapted from Chabay and Sherwood’s textbook always prompts discussion as students compare the different answers written on the whiteboards surrounding the room.
- “Use a laser pointer to determine the thickness of a single hair from your head” (or the spacing of the tracks on a CD). In what is essentially a mini-lab, students spend a few minutes deciding how they will approach the problem, making measurements, and sharing their results with others.
Examples of “Ponderable” Activities
- “How many two-step paces is it across the US?” This activity is done the first day of class as an individual effort. After reporting the wide-ranging answers, students work in ad hoc groups to answer the same question. They are surprised to discover that the range of answers is much smaller, often within the same order of magnitude. This provides an opportunity to discuss the benefits of working in teams, as well as scientific notation, estimations, units, and standards. (The mile was originally defined as 1000 paces of a Roman Centurion.) Some students on their own initiative have started using route-mapping software on the Internet to make very accurate determinations of the distance.
- “How far does a bowling ball travel down the lane before it stops skidding and is only rolling?” This is a very difficult problem and requires a lot of estimation. The insight students gain into what happens to the frictional force when skidding stops and pure rolling begins makes it worth the effort. An Interactive Physics simulation provided for the students gives them confidence in their answers.
- “Design a car radio antenna optimized for your favorite FM station.” This type of activity makes it easy for students to see how physics is involved in their everyday lives. It certainly is not difficult to get students involved in the problem when they have a chance to debate the merits of different radio stations! Many students come back to class the next day having made a measurement on their car that verifies their earlier calculation.